//wwwquoracom/Howistan2x1equalto1cot2x They aren't equal 1 tan^2(x) = (cos^2(x) sin^2(x))/(cos^2(x)) = sec^2(x) 1 cot^2(x) = (sin^2(x) cos^2(x))/(sin^2(x)) = cosec^2(x)Click here👆to get an answer to your question ️ For the equation 1 2x x^2 = tan^2(x y) cot^2(x y)Cos 2x ≠ 2 cos x;
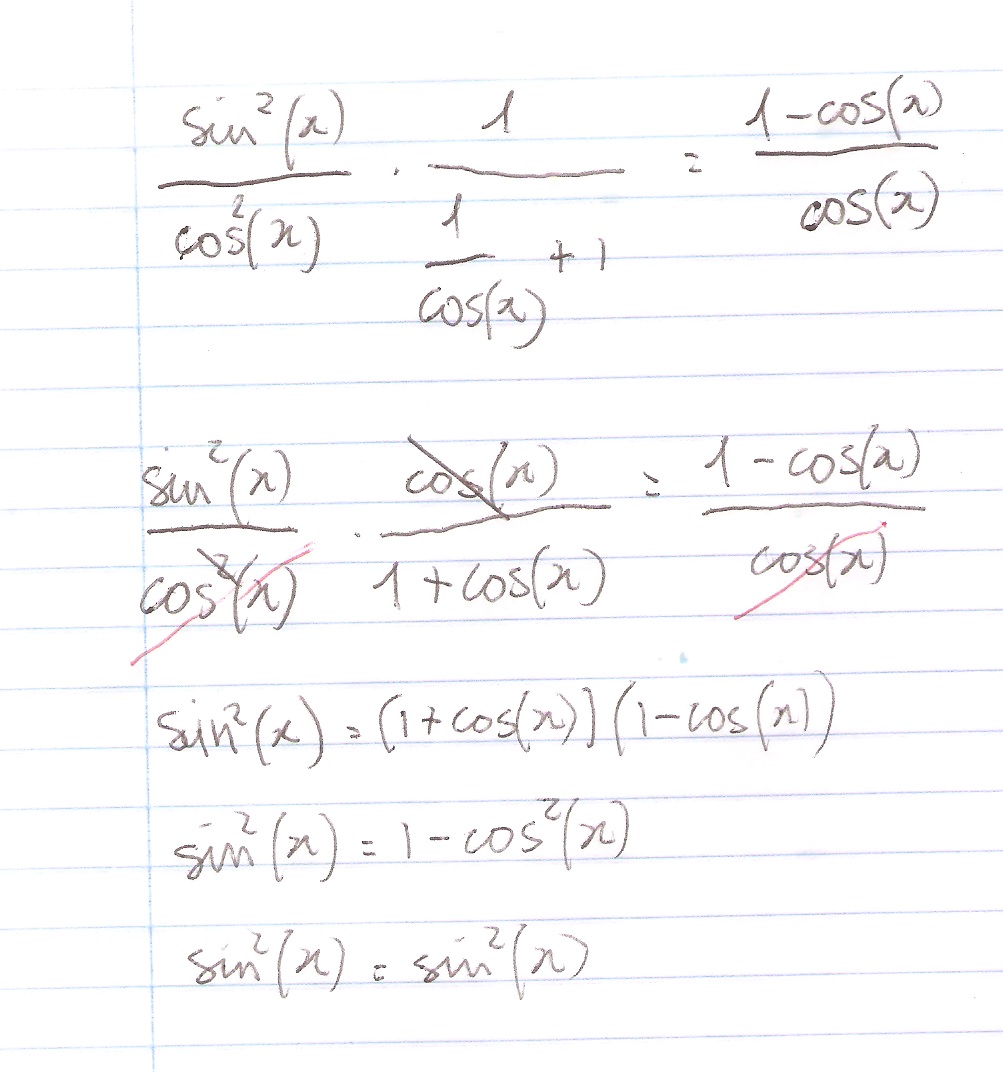
How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic
1 tan 2x/1 cot 2x 1-tanx/1-cotx 2 tan 2x
1 tan 2x/1 cot 2x 1-tanx/1-cotx 2 tan 2x- Get an answer for 'verify (1 tan^2x)/(tan^2x) = csc^2x' and find homework help for other Math questions at eNotes Verify the identity `1/(tan^2x) 1/(cot^2x) = csc^2x 1tan^2x/cot^2x1 = tan^2x sajal3857 is waiting for your help Add your answer and earn points




1 Sin 2x Tan 2x Sec Sec 2 X Csc 2x 1 1 C Gauthmath
Just mess around with the left hand side a bit $$(1\cos^2 x)(1\tan^2 x)$$ We know the following identity $$1\cos ^2 x = \sin^2 x$$ Now, simply replace $1\cos^2 x$ with $\sin^2 x$ $$(\sin^2 x)\cdot(1\tan^2 x)$$ $$\sin^2 x\sin^2 x\cdot\tan^2 x$$ $$\sin^2 x\sin^2 x\cdot\big(\frac{\sin^2 x}{\cos^2 x}\big)$$ $$\sin^2 x \frac{\sin^4 x}{\cos^2 x}$$ Now, just= (12tan^2 x)/(1tan^2 x) tan^2 x , putting tan^2 x = sec^2 x 1 = (12sec^2 x 2)/(1sec^2 x 1 Prove that (i) tan1 {(1 – x2)/2x)} cot1 {(1 – x2)/2x)} = π/2 (ii) sin{tan1 (1 – x2)/2x) cos1 (1 – x2)/ (1 x2)} = 1
D is the differential operator, int is the integration operator, C is the constant of integration Identities tan x = sin x/cos x equation 1 cot x = cos x/sin x equation 2 sec x = 1/cos x equation 3 csc x = 1/sin x equation 4Sin^2x (1cot^2x)=1 distributing the sin^2x sin^2x sin^2xcot^2x = 1 substitute identity of "cot^2x" = cos^2x/sin^2x sin^2x sin^2x (cos^2x/sin^2x) = 1Cosc^2x cot^2x=(1cot^2x)cot^2x=1 (since cosec^2x= 1cot^2x) the exp = log base cot 225 ( 1 ) = y ( say) so ( cot 225)^y= 1 so y =0 ie log(sec^2x tan^2x ) with any base = log( cosec^2x cot^2x) with any base = 0
Prove\\tan^2(x)\sin^2(x)=\tan^2(x)\sin^2(x) prove\\cot(2x)=\frac{1\tan^2(x)}{2\tan(x)} prove\\csc(2x)=\frac{\sec(x)}{2\sin(x)} prove\\frac{\sin(3x)\sin(7x If tan^(1)(cot x)=2x, then find x Please reply fast Its urgent Maths Inverse Trigonometric FunctionsTan 2x = 2 tan x/1 tan2 x = 2 cot x/ cot2 x 1 = 2/cot x – tan x tangent doubleangle identity can be accomplished by applying the same methods, instead use the sum identity for tangent, first • Note sin 2x ≠ 2 sin x;



1 If Fx Sin 2x Cos 2x Sec 2x Csc 2x Tan 2x Cot 2x Gauthmath
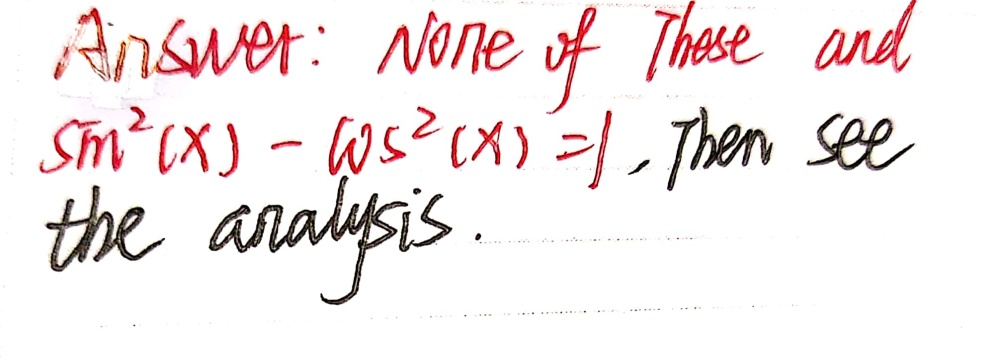



Which One Of The Following Identities Is Incorrect Gauthmath
Tan^4 (x) 1 or (tan^2(x)1)(tan^2x1) then i'm stuck!If ∫cos 8x1tan 2x−cot 2xdx=a cos 8xC then a=−116 a=18 If ∫ cos 8x1 tan 2x−cot 2xdx= a cos 8xC, then A a= −1 16 B a= 1 8 C a= 1 16 D a= −1 8 Please scroll down to see the correct answer and solution guideMore resources available at wwwmisterwootubecom
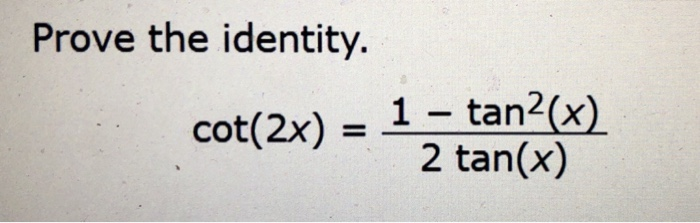



Prove The Identity Cot 2x 1 Tan2 X 2 Tan X Chegg Com



Solved K U 1 Differentiate The Following Choose 4 Only Marks A Y Tan 2x 1 Cot 2x B F X Xsin X 1 X C G X Sec Quot 6x Cos Course Hero
गणना दिया गया है,\(\cot \left( {\frac{\pi }{2} x} \right)\left {1 {{\tan }^2}\left( {\frac{\pi }{2} x} \right)} \right \cot \left Prove the following identities $$(\sec^2 x \tan^2x)(\csc^2 x \cot^2x) = 1 2 \sec^2x \csc^2 x \tag i$$ $$\frac{\cos x}{1\tan x} \frac{\sin x}{1\cot x} = \sin x \cos x \tag {ii}$$ For $(\mathrm i)$ , I initially tried simplifying what was in the 2 brackets but ended up getting 1 1Free integral calculator solve indefinite, definite and multiple integrals with all the steps Type in any integral to get the solution, steps and graph
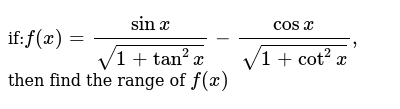



If F X Sinx Sqrt 1 Tan 2x Cosx Sqrt 1 Cot 2x Then




How Do You Prove Tan 2x Secx 1 1 Secx Socratic
Transcript Example 13 Solve tan–1 2x tan–1 3x = π/4 Given tan–1 2x tan 3x = π/4 tan–1 ((2x 3x)/(1 − 2x × 3x)) = π/4 𝟓𝐱/(𝟏 − 𝟔𝐱𝟐) = tan 𝝅/𝟒 We know that tan–1 x tan–1 y = tan–1 ((𝐱 𝐲)/(𝟏 − 𝐱𝐲)) Replacing x by 2x & y by 3x 5x/(1− 6x2) = 1 5x = 1 × (1 – 6x2) 5x = 1 – 6x2 6x2 5x – 1 = 0 6x2 6x – x – 1 = 0 6xQuestion I need to prove the identity (1tan^2x)cot^2x=csc^2x Found 2 solutions by Alan3354, Regrnoth Answer by Alan3354() ( Show Source )B) (tanx 1)(tanx1)/1 tan^2(x) = (sinx/cosx 1)(sinx/cosx 1) / 1/cosx then again I'm stuck!



C2 Solve Tan2x 0 In The Interval 0 180 The Student Room




Ex 3 3 22 Prove Cot X Cot 2x Cot 2x Cot 3x Cot 3x Cot X
Solve for x tan1 (2x/1x2) cot1 (1x2/2x) = π/3;Derivative of tan (2xcot (2x)) \square!Free trigonometric identities list trigonometric identities by request stepbystep




Prove The Following Identities Tan 3 X1 Tan 2 X Cot 3 X1 Cot 2 X 1 2sin 2 Xcos 2 Xsinxcosx




1 Tan 2x 1 Cot 2x 1 Tanx 1 Cotx 2 Prove That Brainly In
Tan 2x ≠ 2 tan x by Shavana GonzalezThis video works through the integral of tan(2x) cot(2x)^2 This type of integral is typically found in a Calculus 1 class *****1/(1tan^2 x) 2tan^2 x/(1tan^2 x) 1/(cot^2 x) = ?




Verify The Identity 1 Tan 2x 1 Cot 2x Csc 2x Chegg Com




I M Having Trouble Solving This Trig Problem 1 1 Tan 2x 1 1 Cot 2x 1 Any Help Wyzant Ask An Expert
tan^2x (1tan^2x)/(1cot^2x) 1) First, notice that both the numerator and denominator are Pythagorean Identities Proceed to change them sec^2x/csc^2x 2) Turn into sine and cosine Then multiply (1/cos^2x)/(1/sin^2x) > 1/cos^2x * sin^2x/1 > tan^2x )Free trigonometry calculator calculate trignometric equations, prove identities and evaluate functions stepbystepEquations Tiger Algebra gives you not only the answers, but also the complete step by step method for solving your equations 1tan^2x/1cot^2x so that you understand better



Trig Identities Hsn Forum




1 6 Trigonometric Review Ppt Video Online Download
Use the double angle formulas to prove the trig identitiesThis function has no specific value It cannot be easily simplified Let's say the question was written with an angle value like A instead of x Because we're going to reuse X, and Y tan (A) = Y/X, where Y is the opposite side of a triangle, and X is the adjacent side Then cot (A) = X/Y = 1/tan (A) So tan^2 (A) cot^2 (A) = (Y/X)^2 (X/Y)^2 = (X^4 Y^4) / (XY)^21 < x < 1 inverse trigonometric functions



Q Tbn And9gcr2jamezvnschsup9wyxdzj0wc0knie4dqfphj6okqiboct8vn1 Usqp Cau
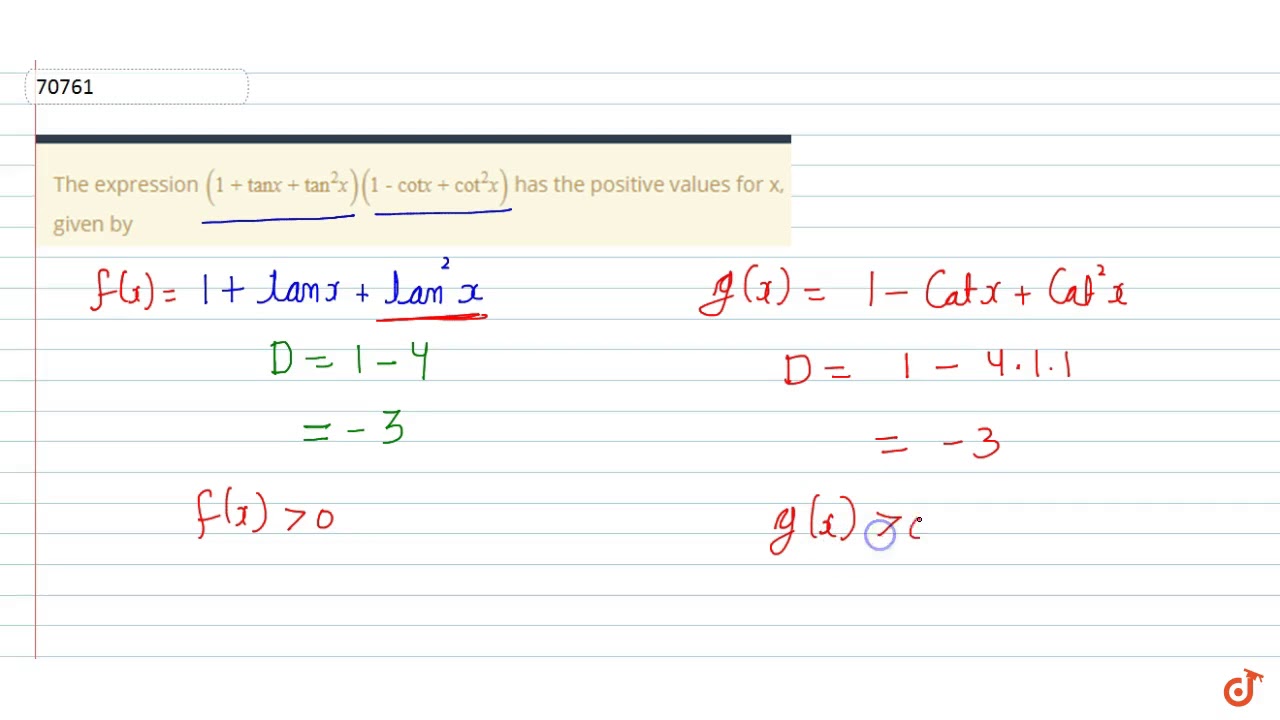



The Expression 1 Tan X Tan 2 X 1 Cot X Cot 2 X Has The Positive Values For X Given Youtube
$$(\cos^2x\sin^2x)(\cos^2x\sin^2x)=\sin^2x\cos^2 x$$ But since $\sin^2x\cos^2x = 1$, we have equality You will have to be careful when dividing though since we cannot divide by zero, so you may have to prove those situations as a special casesMath\dfrac{\csc^2\,x}{1 \tan^2\,x} = \cot^2\,x/math math\text{Left hand side}/math math\dfrac{\csc^2\,x}{1 \tan^2\,x} /math math=\dfrac{\csc^2\,xLegend x and y are independent variables, ;
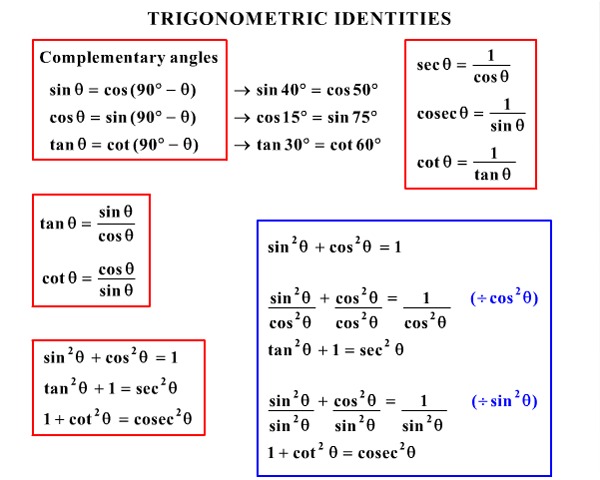



Trig Identities And Formulas Pre Calculus Quiz Quizizz




Find The Derivative Of The Given Function Y Tan 2x 1 Cot 2x I Tried Converting The Original Function In Terms Of Sin And Cos But It Was Still Too Complicated To Be Called Simplified
Best Answer 1 / 1 tan^2x 1 / 1 cot^2x = CPhill Post New AnswerGet an answer for 'how to prove tan^2xcot^2x=2 sec^x1cosec^2x1=2' and find homework help for other Math questions at eNotesAnswer by nerdybill (7384) ( Show Source ) You can put this solution on YOUR website!




The Expression Tan 4x Tan 2x 1 Tan 4x Tan 2x Chegg Com




Find Dy Dx 1 Tan 2x 1 Cot 2x Maths Continuity And Differentiability Meritnation Com
I'm not sure if I should be working on the right side of the equation instead!Comprobación de la identidad trigonométrica csc^2x/(1tan^2x)=cot^2xPara más ejercicios de este tipo, y más, consulta a) Nuestra lista "IDENTIDADES TRIG Use the fundamental identities to simplify the expression cot beta sec beta I used 1tan^2u=secu since cot is the inverse of tan I flipped the tangent, then so it was 1 (1/tan) But the book's answer is the cosecant of beta You can view more similar questions or ask a




Verify Identity 1 Tan 2 X 1 Cot 2 X 1 Tan X 1 Cot X Tan 2 X Youtube




1 1 Tan 2x 1 1 Cot 2x 1 Verifying Trigonometric Identities How To Verify Trig Identities Youtube
Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Step 1 Delete text1 by selecting it and then selecting ⊠ Step 2 Delete conic equation labeled "c" and "d" and then selecting ⊠ Step 3 Enter in input as is f(x)=cot(2x) then press enter button in your keyboard Step 4 Enter in input as is g(x)=(cot^2(x)1)/(2cot(x)) press enter button in CÁC CÔNG THỨC LƯỢNG GIÁC CƠ BẢN Biên soạn và thực hiện vi tính NguyÔn §øc B¸ GV THPT TIỂU LA THĂNG BÌNH I/Các hệ thức cơ bản sin 2 x cos 2 x cosx si




Tan2x ただの悪魔の画像
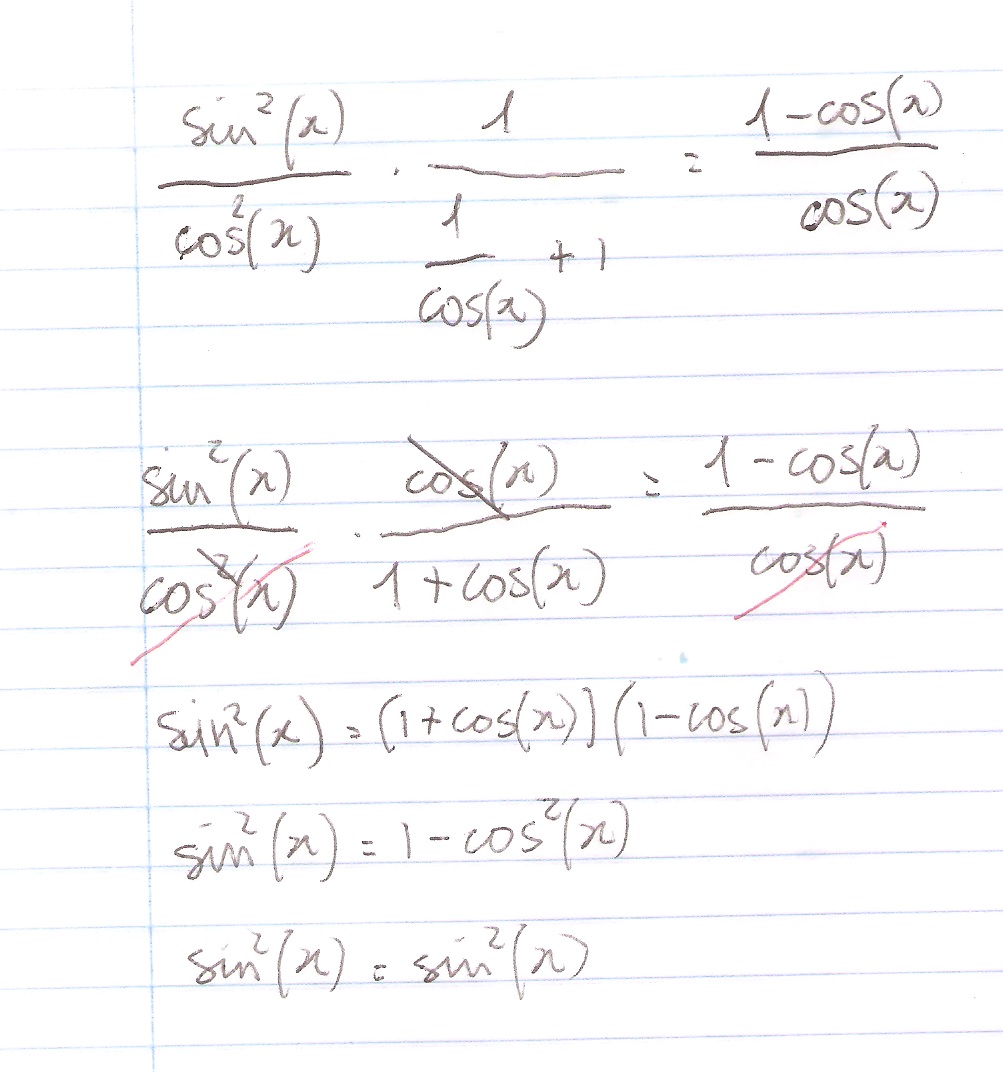



How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic
Click here👆to get an answer to your question ️ The expression (1 tan x tan^2x)(1 cot x cot^2x) has the positive values for x , given byPrecal PreAP tan/cot ws4 Name _____ Graph each for one period Label each quadrant 1 tan 2 y x 2 cot 3 y x 3 tan 1 y x 4 cot 2 1 y x 5 2tan 2 4 y x 6 cot 2 2 y x 7 3tan 2 1 y x 8 2cot 4 1 y xCot ^2 (x) 1 = csc ^2 (x) sin (x y) = sin x cos y cos x sin y cos (x y) = cos x cosy sin x sin y tan (x y) = (tan x tan y) / (1 tan x tan y) sin (2x) = 2 sin x cos x cos (2x) = cos ^2 (x) sin ^2 (x) = 2 cos ^2 (x) 1 = 1 2 sin ^2 (x) tan (2x) = 2 tan (x) / (1 tan ^2 (x)) sin ^2 (x) = 1/2 1/2 cos (2x) cos ^2 (x) = 1/2 1/2 cos (2x)
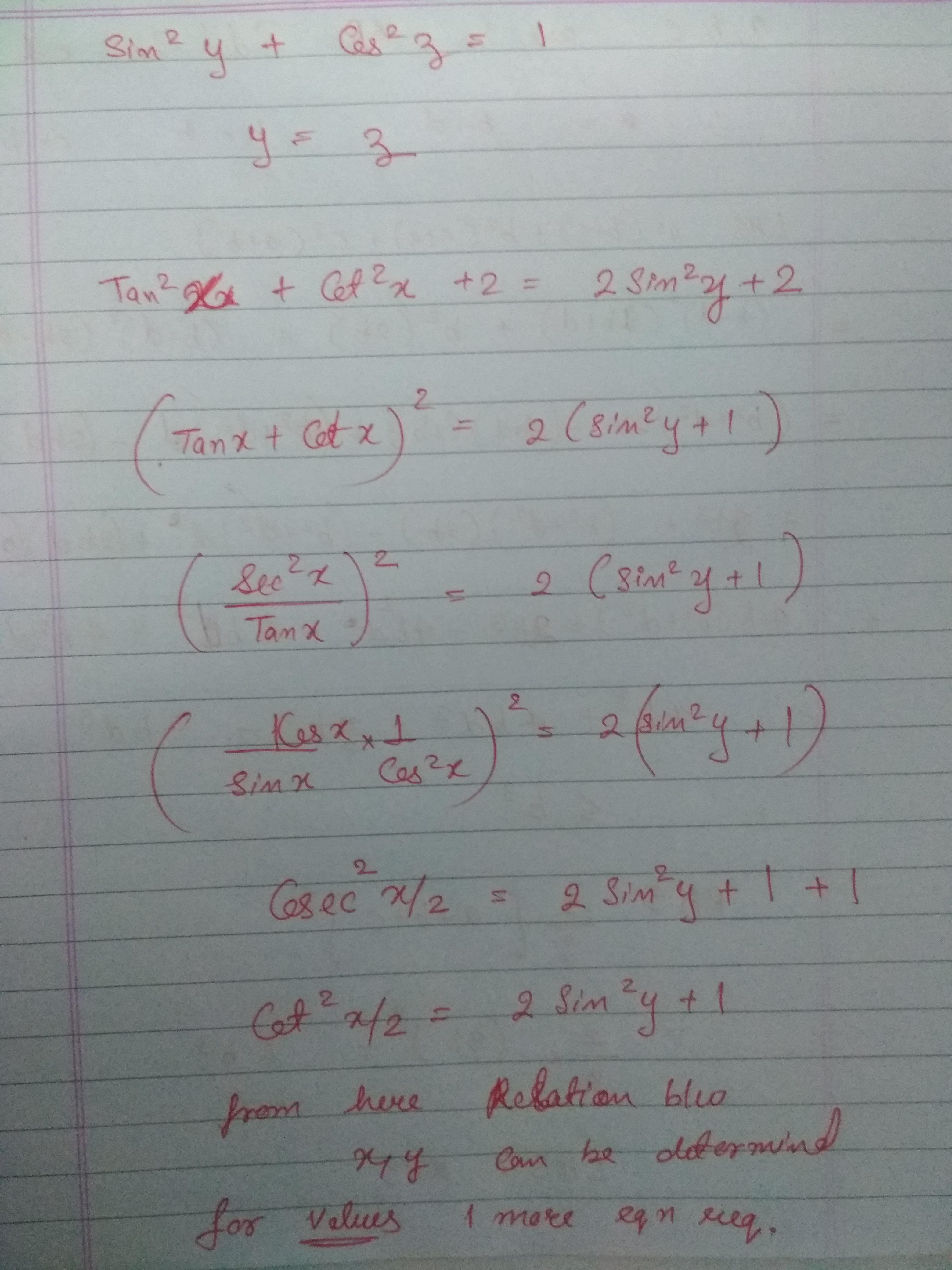



Solve For X Y And Z If Tan 2x Cot 2x 2sin 2y And Sin 2y Cos 2z 1 Askiitians




Trig Identities Ppt Download
Get an answer for 'How do I verify the identity `(cot^2 x 1) /(1cot^2 x) = 12sin^2 x` ``' and find homework help for other Math questions at eNotesVerify that $$ 2\cos^2x1 = \frac{1\tan^2x}{1\tan^2x}$$ Stack Exchange Network Stack Exchange network consists of 178 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careersSolve `tan^(1)((2x)/(1x^(2)))cot^(1)((1x^(2))/(2x))=(pi)/(3),xgt0`Welcome to Doubtnut Doubtnut is World's Biggest Platform for Video Solutions of Phy




Tan 2x Cot 2x 2 Youtube




Qprove That Tan X 2 Tan 2x 4 Tan 4x 8 Cot 8x Cot X Mathematics Topperlearning Com Blpusg55
GrrrrrI could get a little help from the tutors in the Math Lab on campus but we've been instructed not to



How To Prove Cot X Tan X 2cosec 2x Cos 2x Quora




Which Of The Following Equations Are Identities Check All That Apply A Cot 2x Csc2x 1 B Brainly Com



How To Prove That 1 Sin 2x 1 Cotx Cos 2x 1 Tanx Sinxcosx Using Trig Identities Quora




Cot 2x Tan X Cosec 2x Brainly In
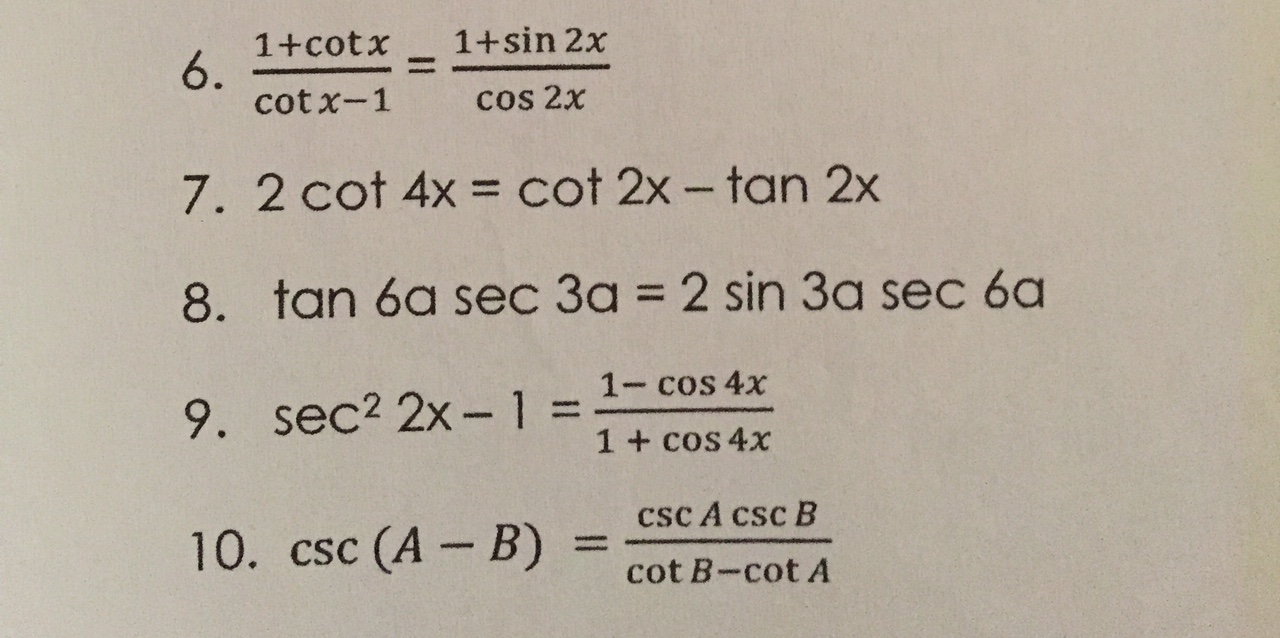



1 Cotx 1 Sin 2x 6 Cotx 1 Cos 2x 7 2 Cot 4x Cot 2x Chegg Com
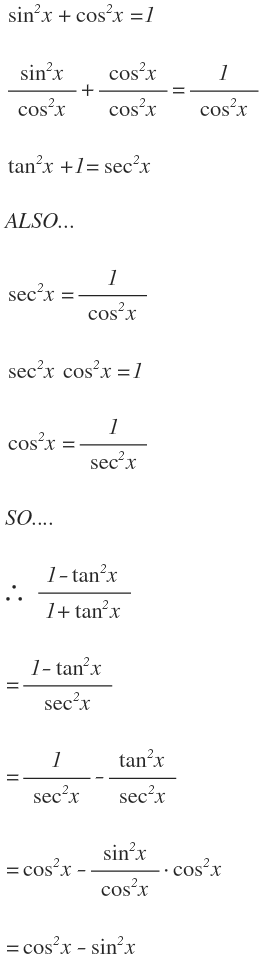



How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic



1
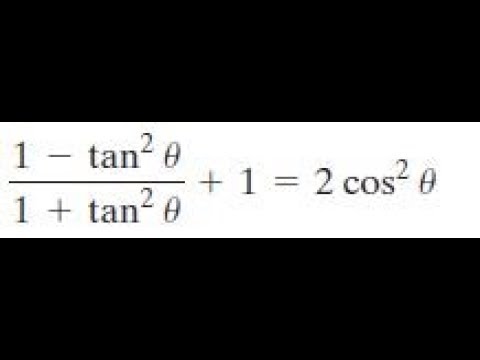



1 Tan 2x 1 Tan 2 X 1 2cos 2 X Youtube



Solved K U 1 Differentiate The Following Choose 4 Only Marks A Y Tan 2x 1 Cot 2x B F X Xsin X 1 X C G X Sec Quot 6x Cos Course Hero




How Do You Simplify Sec 4x Tan 4x Sec 2x Tan 2x Socratic
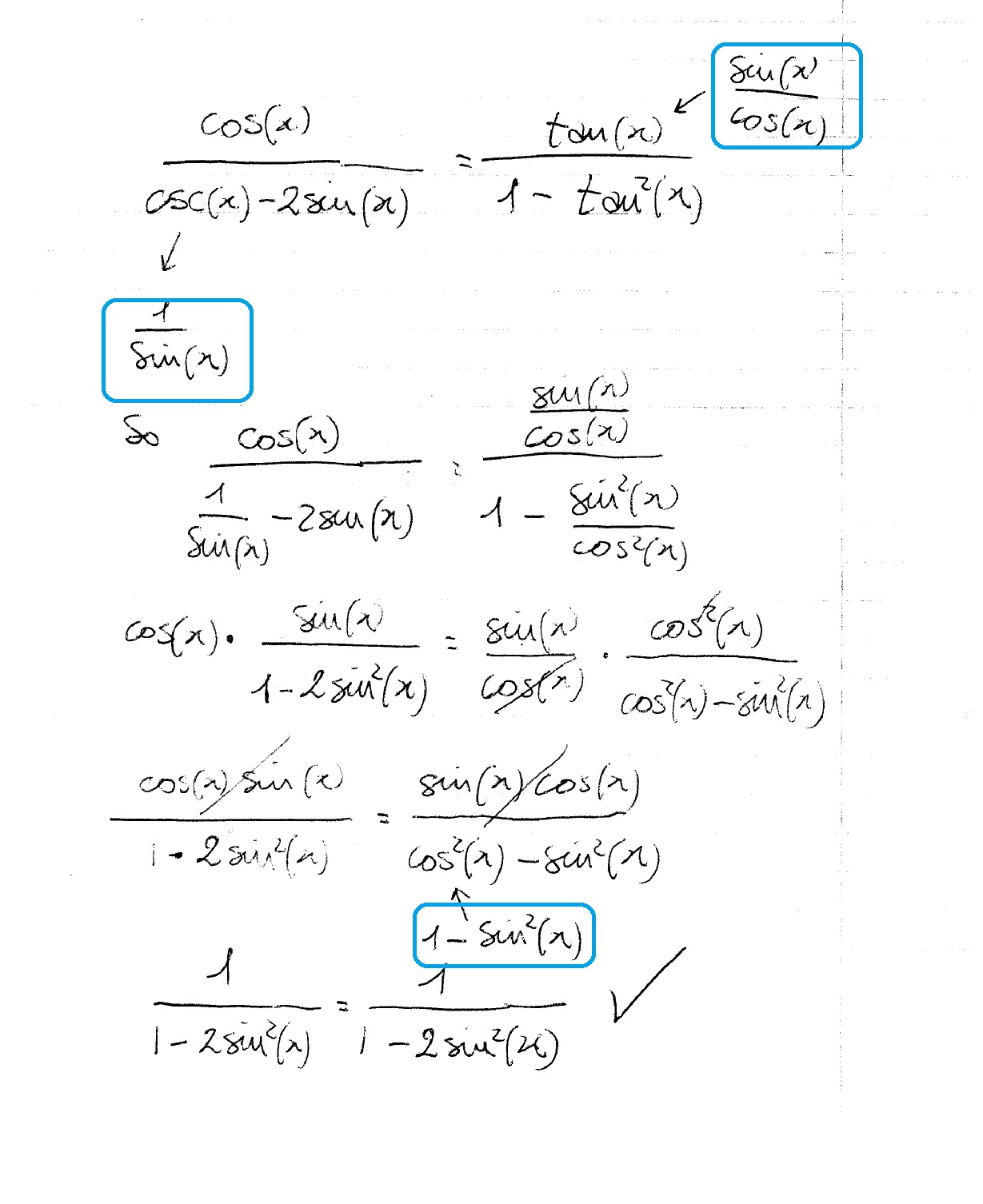



How Do You Prove Cosx Cscx 2sinx Tanx 1 Tan 2x Socratic



Cot2x To Tan2x The Student Room




1 Sin 2x Tan 2x Sec Sec 2 X Csc 2x 1 1 C Gauthmath




1 Cot2x Tan2x Sec2x To See A Detailed Chegg Com




Math34 Trigonometric Formulas




Find Tex I Displaystyle Sf Int Dfrac X Tan X 2 Tan 2x 4 Tan 4x Cot X 8 Brainly In



Http Www Berkeleycitycollege Edu Wp Wjeh Files 12 01 Tri Exercise Identity Pdf



2




11 Sin 2x 2 Tan X 1 Tan X 2 Sin X Cos X 12 Chegg Com
.JPG)



Every Day I M Calculatin I D3 Unit Q Pythagorean Identities




Int 1 Tan 2 X 1 Cot 2 X Dx



What Is The Value Of Tan X 1 Cot X Cot X 1 Tan X Quora
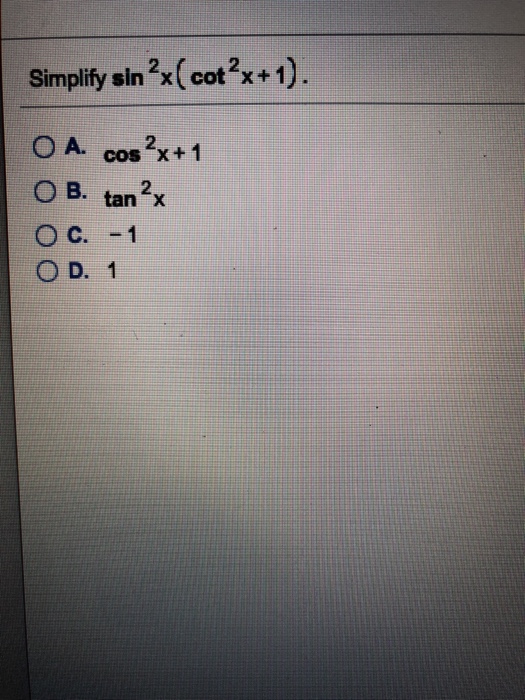



Simplify Sin 2x Cot 2x 1 Oa B Tan 2x Cos X 1 Chegg Com



Q Tbn And9gctg1mv4zqwzzx9es1vyuwisok4cikumrujuyo2nyqlvyw5qkqqv Usqp Cau




Tan2x ただの悪魔の画像




Rd Sharma Solutions For Class 11 Chapter 11 Trigonometric Equations Updated For 21 22 Coolgyan Org




1 Cot 2x S A Sin 2x B Cos 2x C Csc 2x D Sec Gauthmath
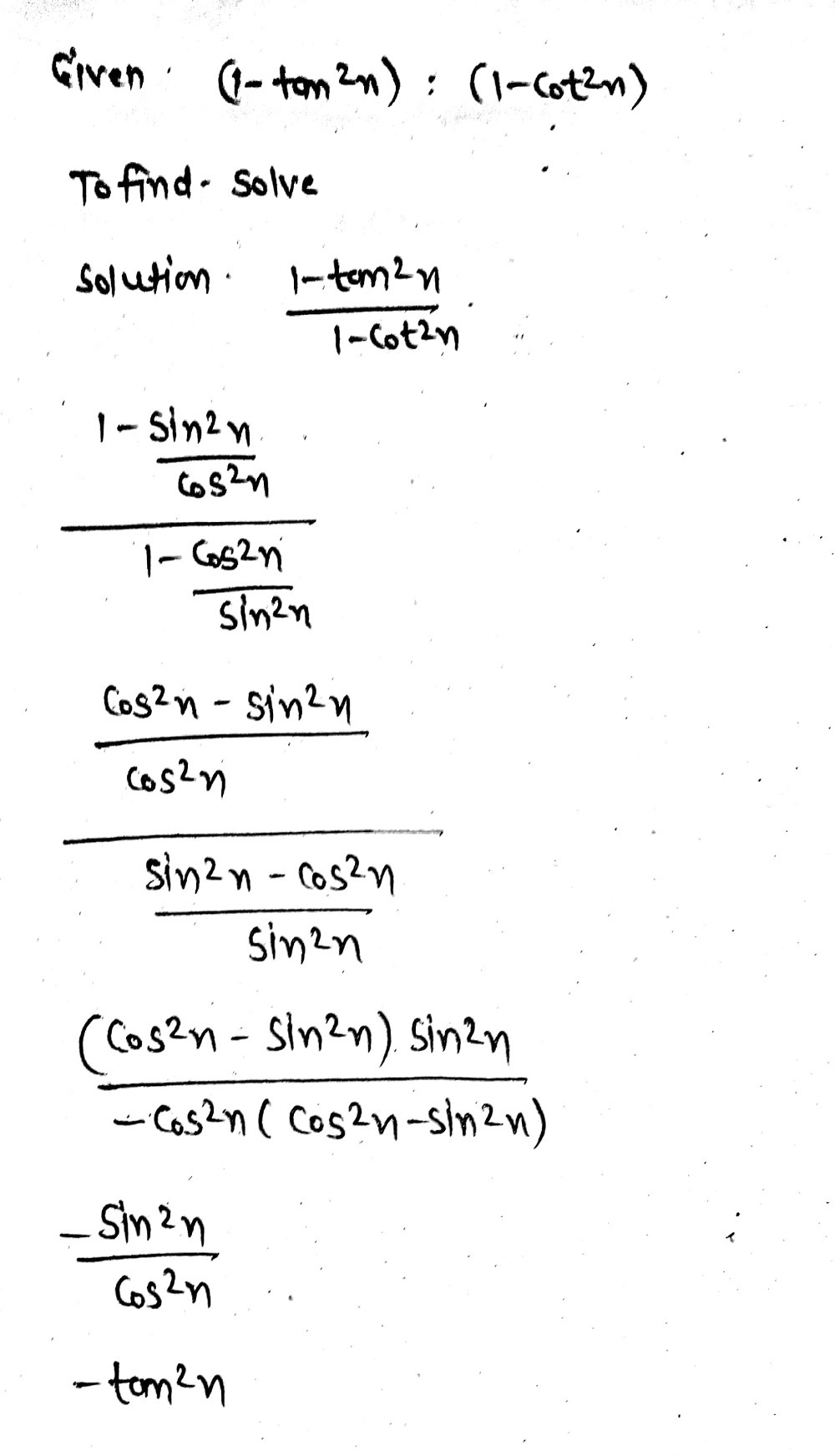



1 Tan 2x 1 Cot 2x Gauthmath




How Do You Prove Cosx Cscx 2sinx Tanx 1 Tan 2x Homeworklib
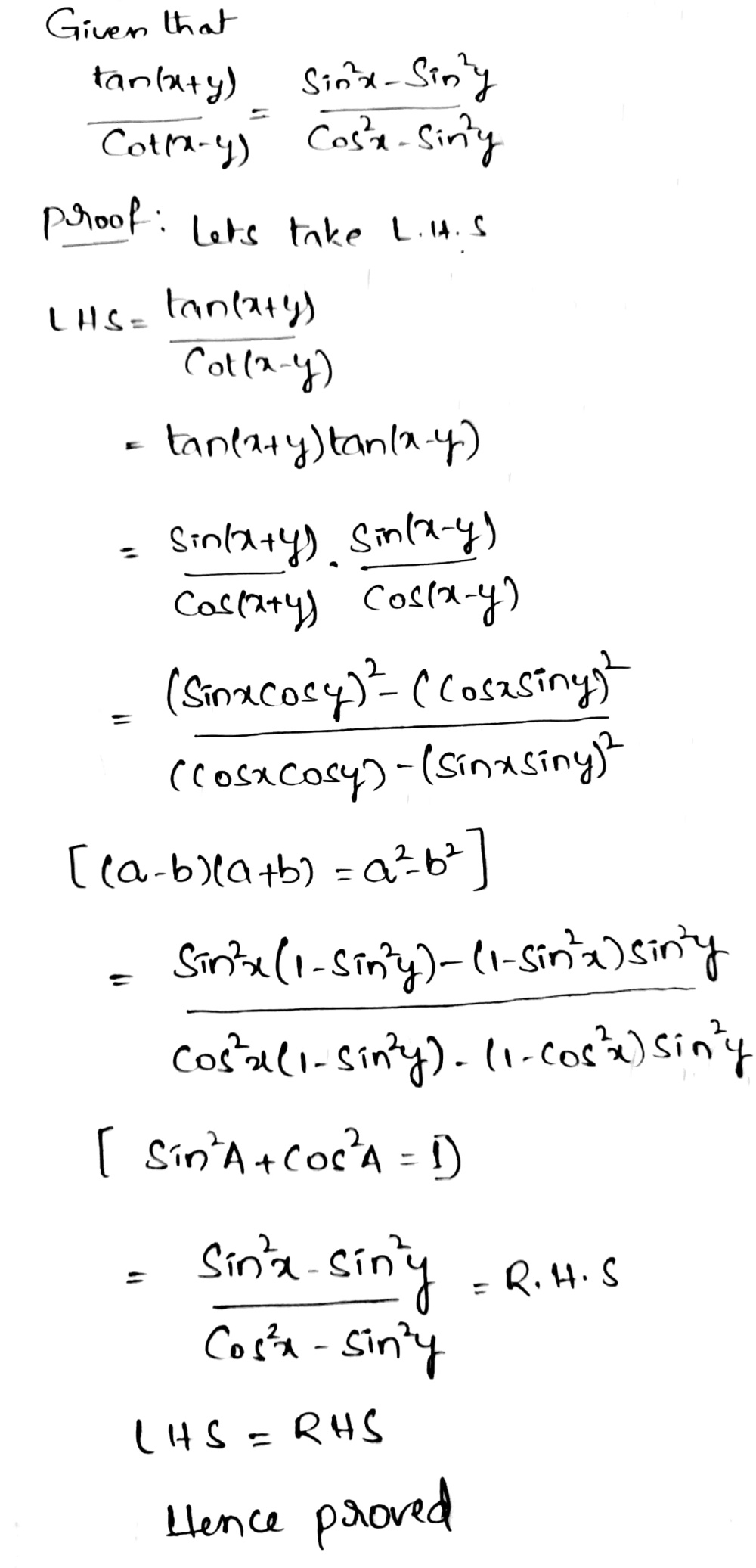



Prove Each Of The Following Frac Tan X Y Cot X Y Frac Sin 2x Sin 2y Cos 2x Sin 2y Frac Tan 2x Tan 2y 1 Tan 2xtan 2y Snapsolve




Tan 2x Cot 2x 2 Youtube



3



Is Cosec 2x Cot 2x True For All Values Of X Quora




Formulas And Identities Flashcards Quizlet




Verify Each Of The Following Identities Csc X Cot Chegg Com



Cos2x Identity




3 Sin Differentiate The Following Functions With Respect Tox 1 Sin 2x 4 Sin 1 Ax




Solve Tan 2x Cot 2x 2 Ana C Ana A Progression Prove That Q Prove That Cosa Cos2a Cos Solve Tan2x Maths Trigonometric Functions Meritnation Com




1 The Set Of Values Of X For Which Tan 3r Tan 2x 1 Tan



Find Dy Dx When Y Sin X X 2 Cot 2x Maths Pyranic




The Value Of F X 6cosxsqrt 1 Tan 2x 2sinxsqrt 1 Cot 2x Where X In 0 2pi Pi Pi 2 3pi 2 May Be




Simplify 1 Sin 2 X 1 Cot 2 X A 1 Csc 2 X Chegg Com



Differentiate The Sec 1 1 Tan 2x 1 Tan 2x W R T X Sarthaks Econnect Largest Online Education Community




Tan 1 Cotx Tan 1 Cot2x




The Simple Proof Of Cosec 2 X 1 Cot 2 X Maths Made Interesting
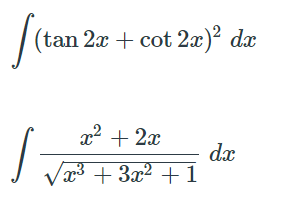



Answered Tan 2x Cot 2x Dx X2 2x Dx 3 3x Bartleby




Tan 3x 1 Tan 2x Cot 3x 1 Cot 2xhope It Helps U Welltq Brainly In
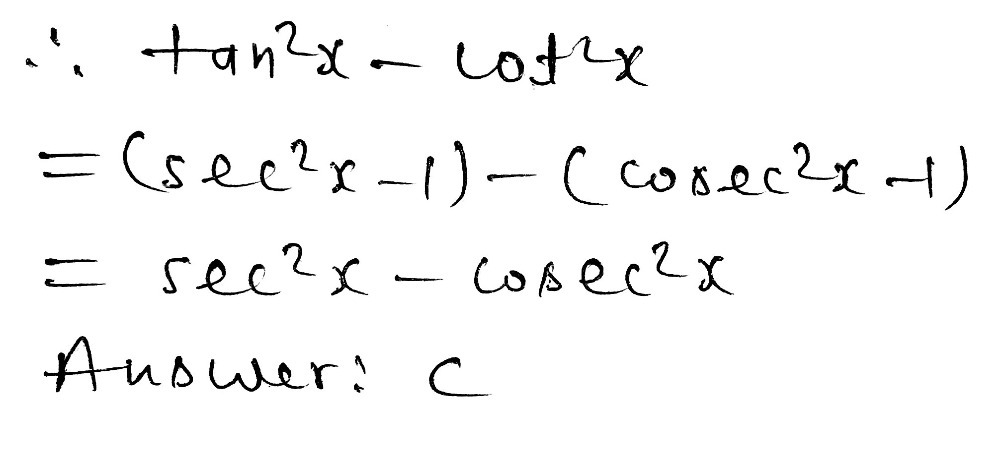



Use Trig Identities To Simplify Tan 2x Cot 2x A Gauthmath
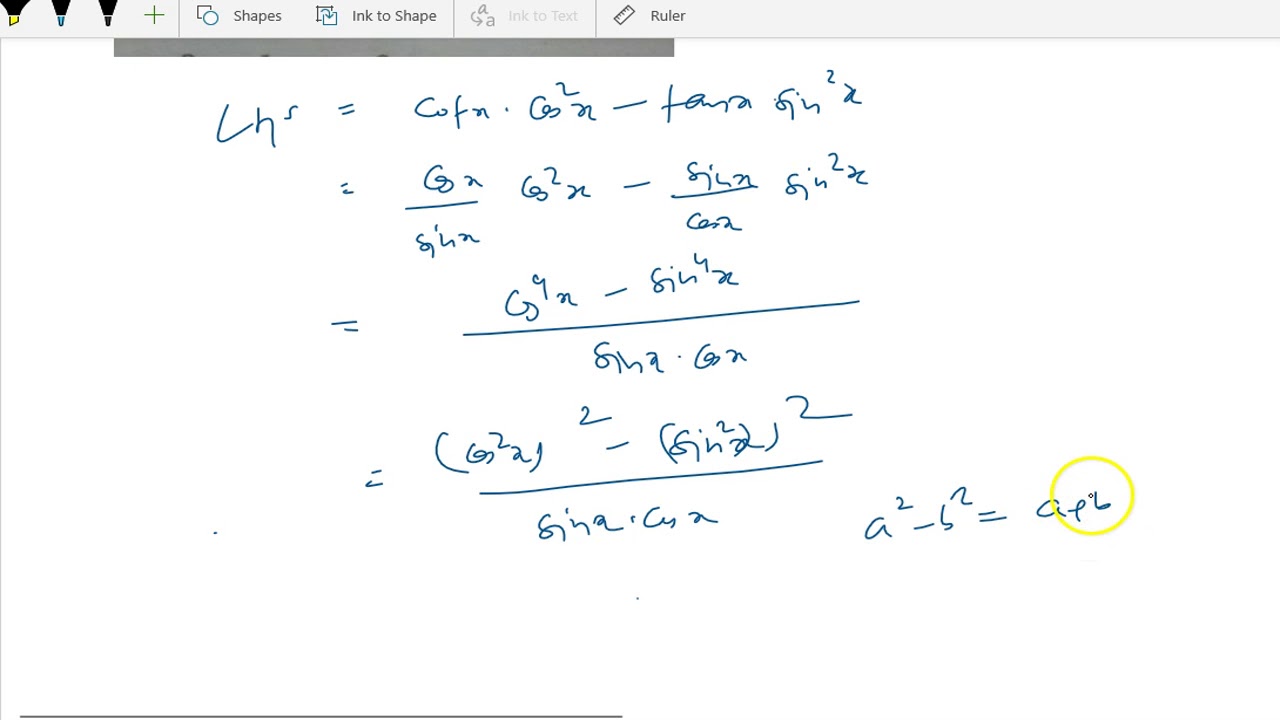



Cot X Cos 2 X Tan X Sin 2 X 2 Cot 2x Youtube




Int Cos8x 1 Tan2x Cot2x Dx Youtube



Sites Math Washington Edu Putnam Handouttrig Pdf




Misc 44 Mcq Value Fo Tan 1 2x 1 1 X X2 Dx Is



Math Problems Simplifying With Trigonometry Identities And Then Integration



A Trig Identity



Prove The Identity Tan X 1 Cot X Cot X 1 Tan X Sec X Cosec X 1 Sarthaks Econnect Largest Online Education Community




1 Tan2 1 Cot2 1 Tan 1 Cot 2 Tan2 Maths Meritnation Com
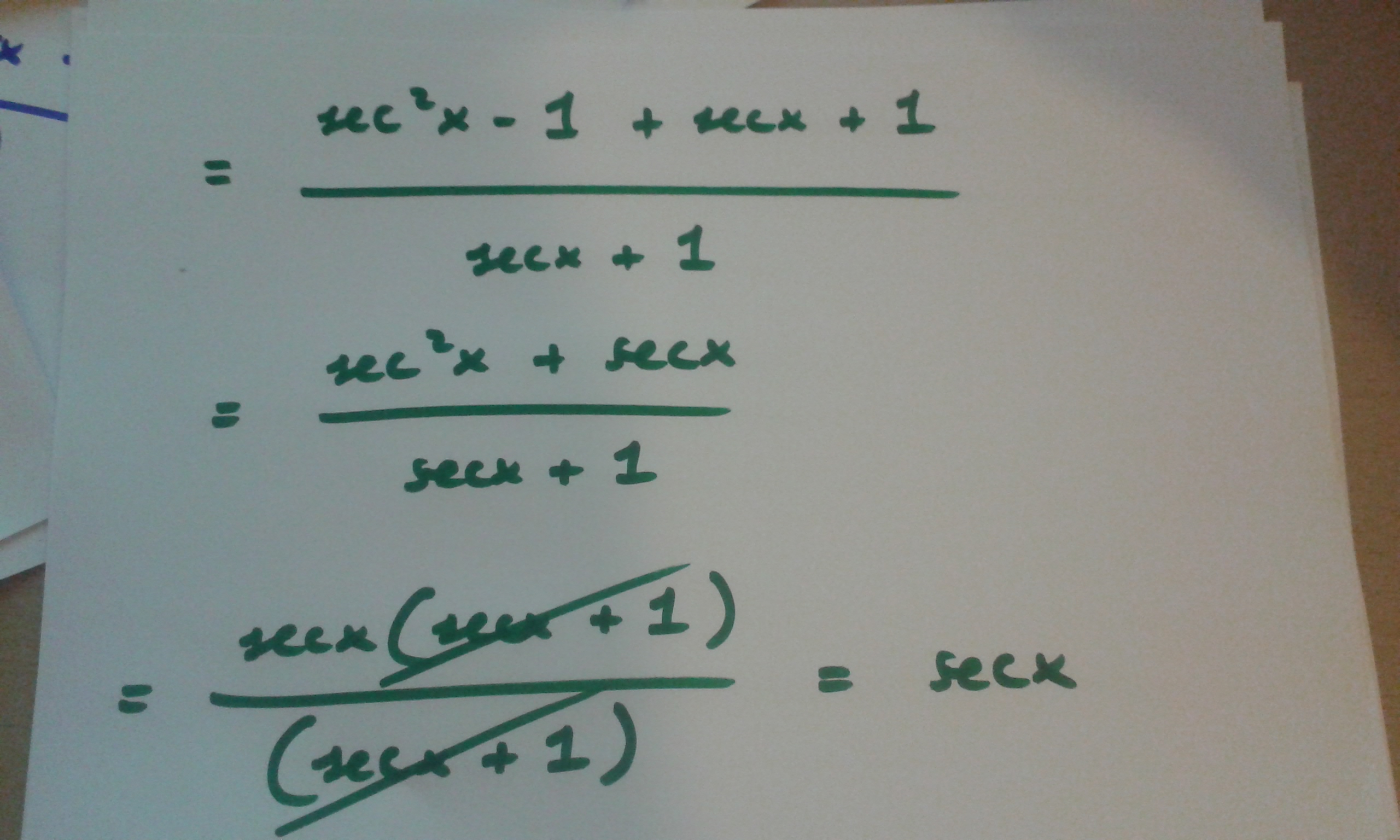



How Do You Prove Tan 2x Secx 1 1 Secx Socratic




1 Tan 2x 1 Cos 2x Sin 2x 2sin 4x 1 Sin 2x Trigonometric Identities Mcr3u Youtube




Simplify This Trig Function 1 Tan 2x Csc 2x Youtube




Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube




Please Solve It Or Show That 1 Tan2x 1 Cot2x 1 Sin2xa Sin4x Maths Introduction To Trigonometry Meritnation Com
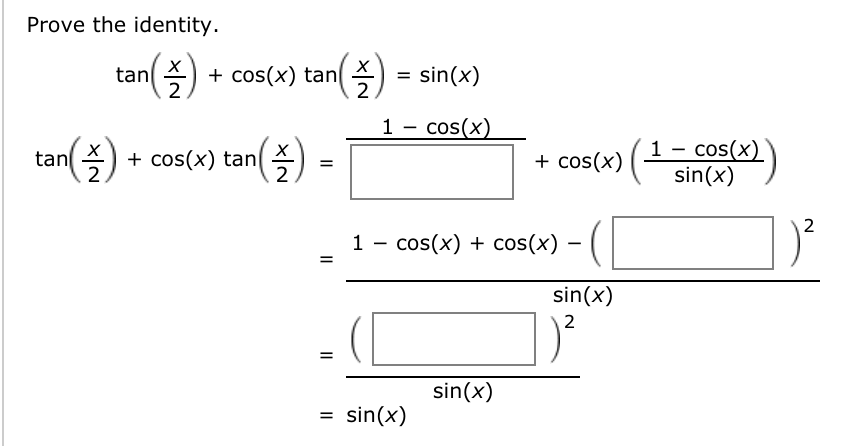



Prove The Identity Cot 2x 1 Tan2x 2 Tan X Chegg Com



If Cot 2x 3 Tan X 3 Cosec Kx 3 Then What Is The Value Of K Quora



Www Jstor Org Stable



How Do You Simplify 1 Tan 2x 1 Cot 2x Socratic



What Is The General Solution Of X For Tan X Tan2x 1 Quora
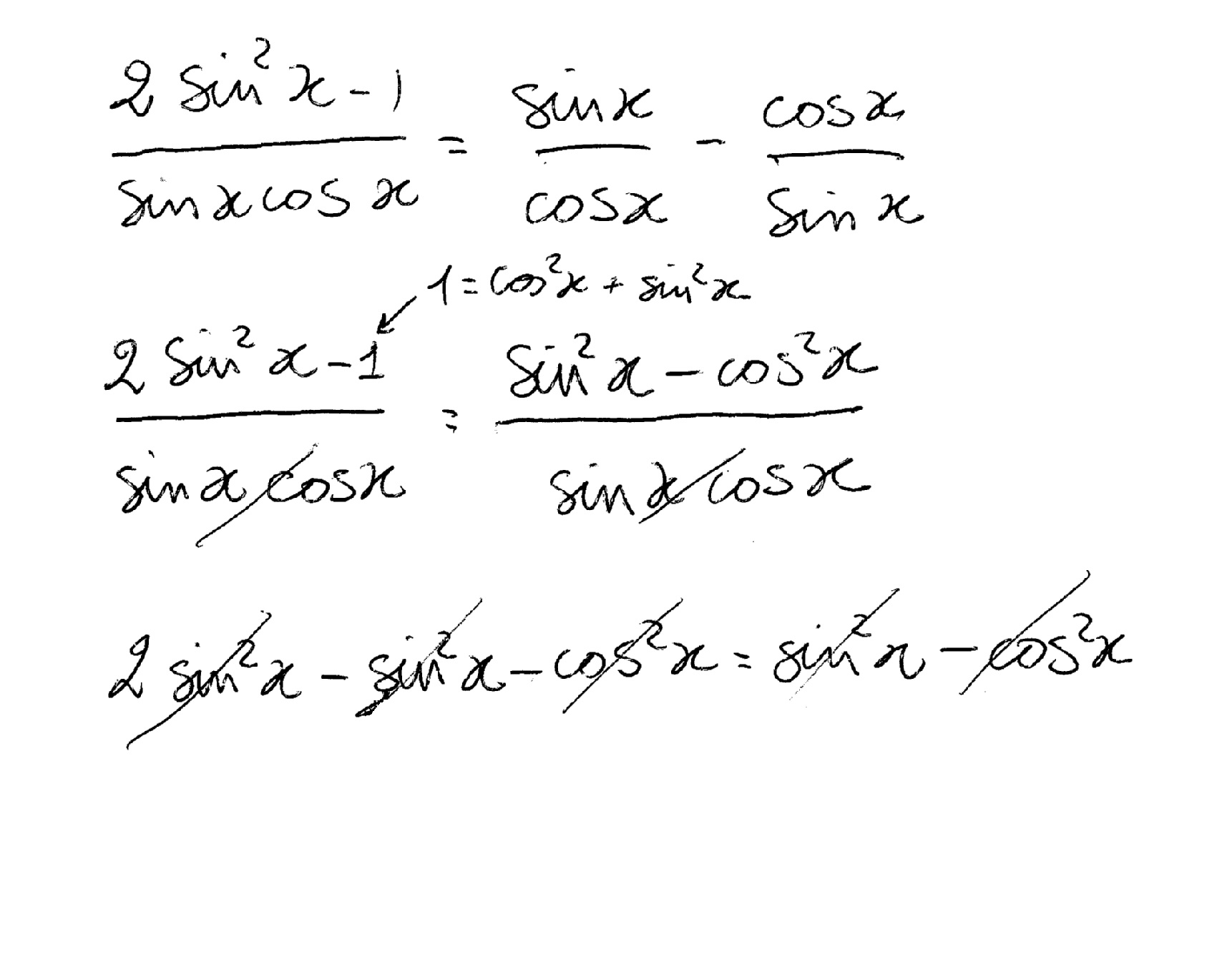



How Do You Prove 2sin 2x 1 Sinxcosx Tanx Cotx Socratic



Http Www Mpsaz Org Mtnview Staff Clpavlovic Collegealgebra Resources Files Assignment 6 3 Day 1 3 Worksheet Key Pdf



Permanent Tambur Mordant Cot 1 Tan Lmvdesigns Com
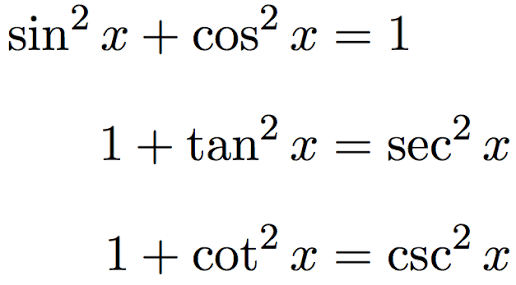



How Do You Verify Csc 2xcot 2x Csc 2x Csc 4x Socratic




Cos2x Sin2x 1 1 Tan2x Sec2x Cot2x 1 Csc2x Cofunction




Math Rescue Trigonometry Proving Trigonometric Identities Math Methods Trigonometry Help Free Math Help
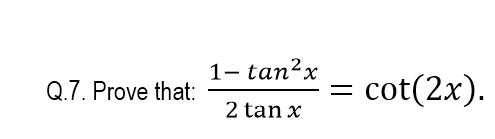



Prove That 1 Tan 2 X 2 Tan X Cot 2x Chegg Com




Integration Trig Identities Ppt Download
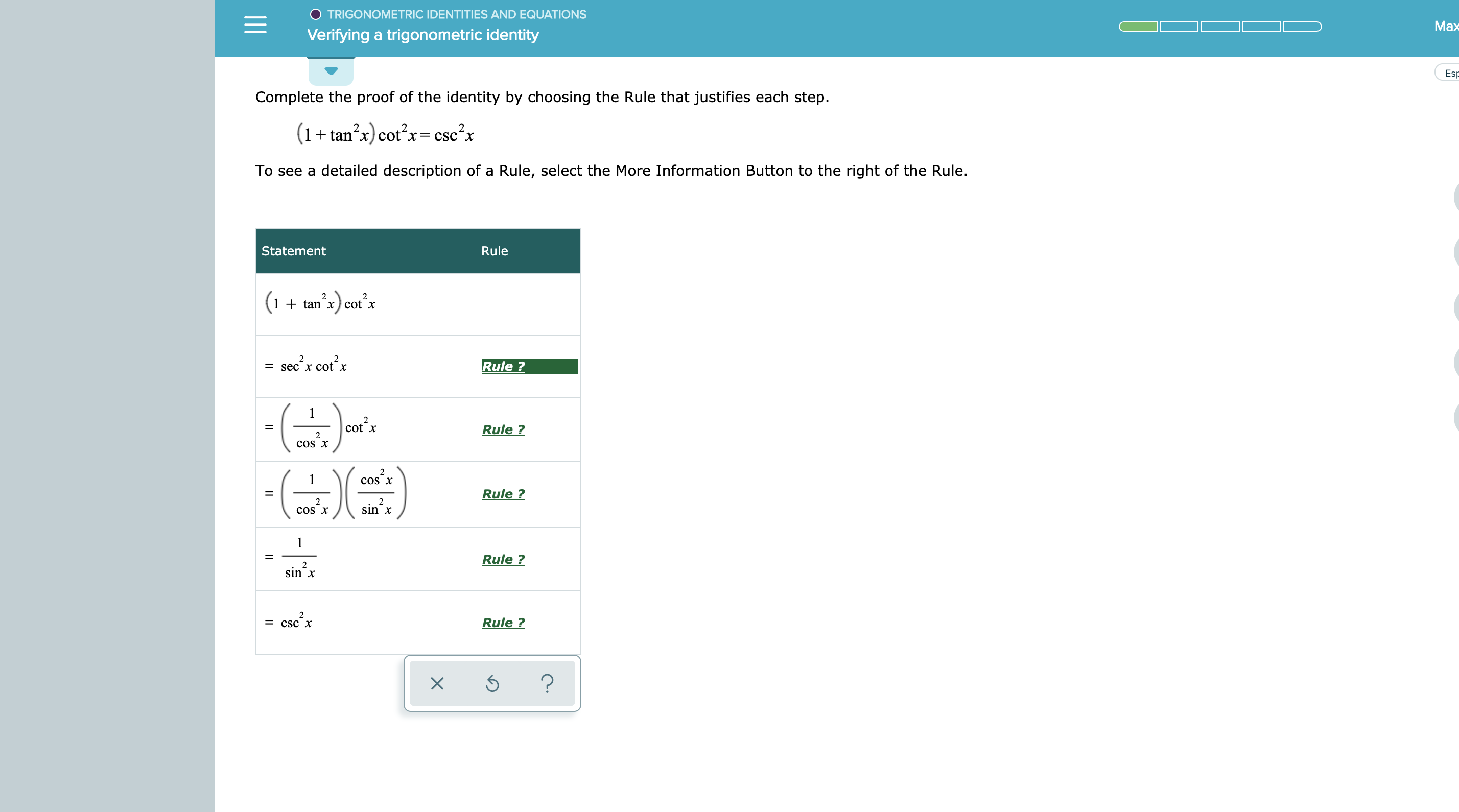



Answered Trigonometric Identities And Equations Bartleby




Verify That The Equation Is An Identity Tan 2x Cot Chegg Com



0 件のコメント:
コメントを投稿