Trig identities tan^2 theta 692398-Trig identities tan^2 theta

Trig identities Trigonometric identities are equations that are used to describe the many relationships that exist between the trigonometric functions Among other uses, they can be helpful for simplifying trigonometric expressions and equations The following shows some of the identities you may encounter in your study of trigonometryIn this video I will solve 3tan^3(theta)=tan(theta), theta=?Basic Trig Identities The basic trig identities or fundamental trigonometric identities are actually those trigonometric functions which are true each time for variablesSo, these trig identities portray certain functions of at least one angle (it could be more angles) It is identified with a unit circle where the connection between the lines and angles in a Cartesian plane

1 Given The Triangle Below Calculate The Following Chegg Com

Trig identities tan^2 theta

Trig identities tan^2 theta-TRIGONOMETRIC IDENTITIES A N IDENTITY IS AN EQUALITY that is true for any value of the variable (An equation is an equality that is true only for certain values of the variable) In algebra, for example, we have this identity ( x 5) ( x − 5) = x2 − 25The subtraction of the tan squared of angle from secant squared of angle is equal to one and it is called as the Pythagorean identity of secant and tangent functions $\sec^2{\theta}\tan^2{\theta} \,=\, 1$ Popular forms The Pythagorean identity of secant and tan functions can also be written popularly in two other forms $\sec^2{x}\tan^2{x

Complex And Trigonometric Identities Introduction To Digital Filters

Purplemath In mathematics, an "identity" is an equation which is always true These can be "trivially" true, like "x = x" or usefully true, such as the Pythagorean Theorem's "a 2 b 2 = c 2" for right trianglesThere are loads of trigonometric identities, but the following are the ones you're most likely to see and use1tan2θ=sec2θ 1 tan 2 θ = sec 2 θ The second and third identities can be obtained by manipulating the first The identity 1cot2θ = csc2θ 1 cot 2 θ = csc 2 θ is found by rewriting the left side of the equation in terms of sine and cosine Prove 1cot2θ = csc2θ 1 cot 2 θ = csc 2 θ Explanation We will use the identity tanθ = 2tan(θ 2) 1 − tan2(θ 2) Let x = tan(θ 2) then tanθ = 2x 1 −x2 or tanθ(1 −x2) = 2x or −tanθx2 −2x tanθ = 0 or tanθx2 2x − tanθ = 0 Now using quadratic formula x = −2 ± √22 − 4 × tanθ ×( − tanθ) 2tanθ x = −2 ± √4 4tan2θ 2tanθ or

Using Trig Identities to Solve a Quadratic in Sin x Category Mathematics In the first of this pair of Casio videos, the identity sin 2 x cos 2 x≡ 1 is used to solve fully the equation 9sin 2 x 21sinx = 3cos 2 x 12 The second video explores how a graphical calculator can be used to find solutions of the equation by plotting both sides of the equation we are trying to solve, andTrig Identities and Approximations From our first identity \textcolor{blue}{\sin ^2 \theta} \textcolor{limegreen}{\cos ^2 \theta} \equiv 1, we have two new identities Make sure you are happy with the following topics before continuing Basic Trig IdentitiesStart studying trig identities (6163) Learn vocabulary, terms, and more with flashcards, games, and other study tools

Trigonometry Examples Verify the Identity (sin (theta)^2tan (theta))/ (cos (theta)^2cot (theta))=tan (theta)^2 Start on the left side Convert to sines and cosines Tap for more steps Write tan ( θ) tan ( θ) in sines and cosines using the quotient identityTrigonometric Identities Solver \square!SubsectionUsing Trigonometric Ratios in Identities 🔗 Because the identity 2x2 − x − 1 = (2x 1)(x − 1) 🔗 is true for any value of x, it is true when x is replaced, for instance, by cosθ This gives us a new identity 2cos2θ − cosθ − 1 = (2cosθ 1)(cosθ − 1) 🔗

1 Tan 2x 1 Tan 2 X 1 2cos 2 X Youtube

Bestmaths Online Proof 4

Start studying Ch 5 Trig Identities Learn vocabulary, terms, and more with flashcards, games, and other study toolsPythagorean Identities sin 2 a cos 2 a = 162 Trigonometric identities (EMBHH) An identity is a mathematical statement that equates one quantity with another Trigonometric identities allow us to simplify a given expression so that it contains sine and cosine ratios only This enables us to solve equations and also to prove other identities

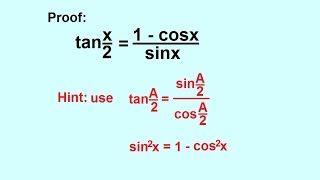
Precalculus Trigonometry Trig Identities 34 Of 57 Proof Half Angle Formula Tan X 2 Youtube

Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download

The two sides reduce to the same expression, so we can conclude this is a valid identity In the last step, we used the Pythagorean Identity, \(\sin^2 \theta \cos^2 \theta =1\), and isolated the \(\cos^2 x=1−\sin^2x\) There are usually more than one way to verify a trig identitySolving Word Problems Using Trigonometric Identities Step 1 Understanding the question and drawing the appropriate diagram are the two most important things to be done in solving word problems in trigonometry23 godz temu I would like to know which trig identities to use to simplify these two equations on the LHS to the RHS This appeared as a solution in my textbook with some steps skipped $$\frac{cos(n\theta)cos(\

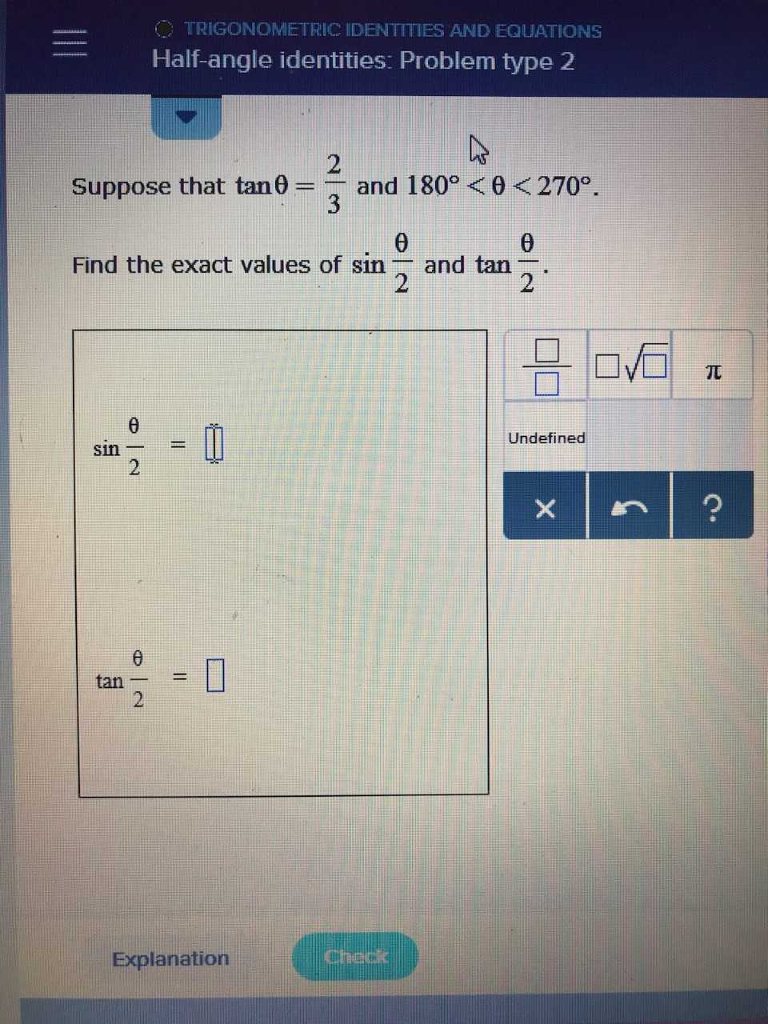
Trigonometric Identities And Equations Half Angle Chegg Com

Cos 2 1 Tan 2 1 Youtube

$\tan^2{\theta} \,=\, \sec^2{\theta}1$ The square of tan function equals to the subtraction of one from the square of secant function is called the tan squared formula It is also called as the square of tan function identity Introduction The tangent functions are often involved in trigonometric expressions and equations in square form TheMy issue is understanding the connection between those rules and what exists on the RHS within equation $(1)$ Apologies for any confusion on thisVisit http//ilectureonlinecom for more math and science lectures!In this video I will solve tan^2(theta)4=0, theta=?

List Of Trigonometric Identities Wikipedia

How Does The Trigonometric Identity 1 Cot 2 Theta Csc 2 Theta Derive From The Identity Sin 2 Theta Cos 2 Theta 1 Mathematics Stack Exchange

 Trigonometric Identities Sine, tangent, cotangent and cosecant in mathematics an identity is an equation that is always true Meanwhile trigonometric identities are equations that involve trigonometric functions that are always true This identities mostly refer to one angle labelled θIdentities expressing trig functions in terms of their supplements Sum, difference, and double angle formulas for tangent The half angle formulas The ones for sine and cosine take the positive or negative square root depending on the quadrant of the angle θ/2 For example, if θ/2 is an acute angle, then the positive root would be usedAll the trigonometric identities on one page Color coded Mobile friendly With PDF and JPG downloads Trig Identities Download PDF Download JPG Reciprocal Identities I highly recommend this 3minute video $$ \tan(2\theta) = \frac{2\tan\theta}{1\tan^2\theta} $$

How Do You Prove Tan 2x Secx 1 1 Secx Socratic

Rd Sharma Solutions For Class 10 Chapter 6 Trigonometric Identities Exercise 6 1 Get Pdf

 Just like that we have an identity with two of the other trig functions 1 cot 2 (θ) = csc 2 (θ) Last but not least, we have two more trig functions we have to cover Tan and SecThe Pythagorean Identities sin cos 12 2θ θ = 1 tan sec =2 2θ θ 1 cot csc =2 2θ θ Using Fundamental Identities to Verify Other Identities The fundamental trig identities are used to establish other relationships among trigonometric functions To verify an identity we show that one side of the identity can be simplified so that isFree math lessons and math homework help from basic math to algebra, geometry and beyond Students, teachers, parents, and everyone can find solutions to their math problems instantly

3

Sample Problems Cos 2 X Tan2 X Tan 2 Csc 2 Tan Sec X Tan X Cos X Sin 4 X Cos 4 X 1 2 Cos 2 X Pdf Free Download

 You can check some important questions on trigonometry and trigonometry all formula from below 1 Find cos X and tan X if sin X = 2/3 2 In a given triangle LMN, with a right angle at M, LN MN = 30 cm and LM = 8 cm Calculate the values of sin L, cos L, and tan L 3For any value of \(x\), this equation is true Trig identities are sort of like puzzles since you have toAn "identity" is something that is always true, so you are typically either substituting or trying to get two sides of an equation to equal each otherThink of it as a reflection;

Sample Problems Cos 2 X Tan2 X Tan 2 Csc 2 Tan Sec X Tan X Cos X Sin 4 X Cos 4 X 1 2 Cos 2 X Pdf Free Download

Trigonometric Identities And Equations Ppt Download

For the sake of clarification, I'm also aware of the double angle rules and how they are used to obtain $\tan^2(\frac{\theta}{2})$;Trig identities stuck solving $\tan^2\theta = \frac 32 \sec\theta$ Ask Question Asked 4 years, 4 months ago Active 4 years, 4 months ago Viewed 156 times 2 0 $\begingroup$ Solve the equation on the interval $0\leq \theta < 2\pi$ $$\tan^2 \theta = \frac{3}{2}\sec \theta $$Trigonometric identities are equalities involving trigonometric functions An example of a trigonometric identity is \sin^2 \theta \cos^2 \theta = 1 sin2 θcos2 θ = 1 In order to prove trigonometric identities, we generally use other known identities such as Pythagorean identities

How Do You Prove The Identities Cosx Secx Sinx Cscx Sec 2x Tan 2x Socratic

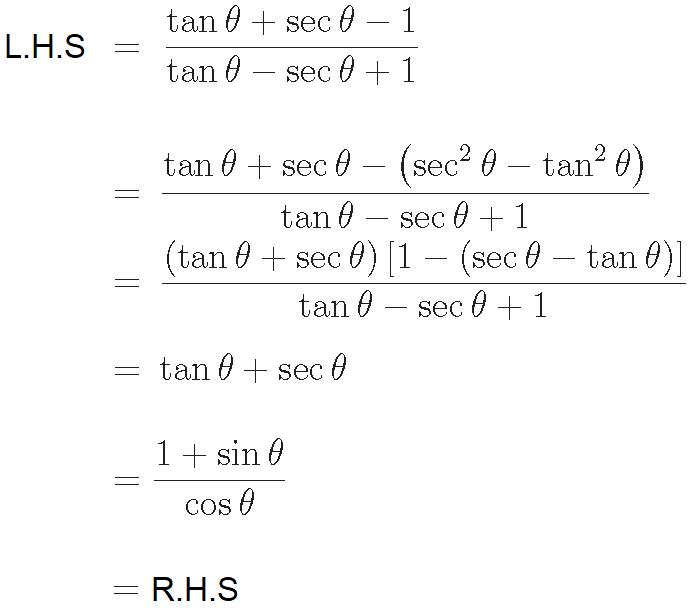
Basic Trigonometric Identities

Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Tan θ = 1/Cot θ or Cot θ = 1/Tan θ;Cos^2 x sin^2 x = 1 sin x/cos x = tan x You want to simplify an equation down so you can use one of the trig identities to simplify your answer even more some other identities (you will learn later) include cos x/sin x = cot x 1 tan^2 x = sec^2 x 1 cot^2 x = csc^2 x hope this helped!

Establish The Identity 1 Sin 2 X 1 Tan 2 X 1 Youtube

10 1 Reciprocal And Pythagorean Identities Mathematics Libretexts

 If you use this trig substitution, keep in mind the trig identity secant squared of theta minus 1 equals the tangent squared of theta (sec^2(theta) – 1 = tan^2(theta)) Example #1, Continued Let's go back to our example of (1 / the square root of (1 – x^2))dx Because we have 1 – x^2, that's like 1^2 – x^2Trigonometric Equation Calculator \square!θ θ = hyp adj r x 1 tan sin cos θ θ θ = = = opp adj y x cot tan θ θ = = = adj opp x y 1 Sum or difference of two angles 2 sin(a ± b) = sin acos b ±cos asin b cos(a ±b) = cosacosbmsinasinb tan( ) tan tan tan tan a b a b a b ± = ± 1m Double angle formulas 2tan tan tan 2 1 2 θ θ θ = − sin 2 θ= sin cos cos2θ = 2cos2 θ −1 cos

How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic

1 Given The Triangle Below Calculate The Following Chegg Com

Like looking in a mirror An example of a trig identity is \(\displaystyle \csc (x)=\frac{1}{\sin (x)}\);The figure at the right shows a sector of a circle with radius 1 The sector is θ/(2 π) of the whole circle, so its area is θ/2We assume here that θ < π /2 = = = ⁡ = ⁡ The area of triangle OAD is AB/2, or sin(θ)/2The area of triangle OCD is CD/2, or tan(θ)/2 Since triangle OAD lies completely inside the sector, which in turn lies completely inside triangle OCD, we haveCos θ = 1/Sec θ or Sec θ = 1/Cos θ;

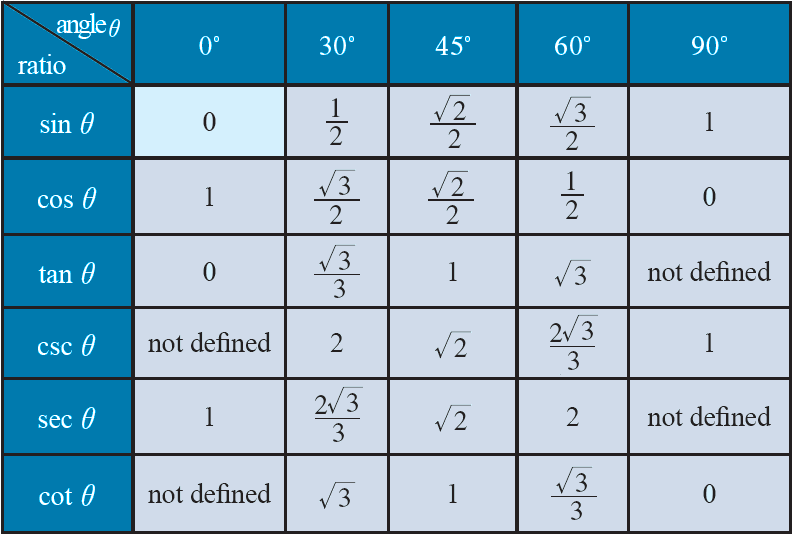
Trigonometric Identities

Trigonometric Identities A Plus Topper

 We now proceed to derive two other related formulas that can be used when proving trigonometric identities It is suggested that you remember how to find the identities, rather than try to memorise each one Dividing sin 2 θ cos 2 θ = 1 through by cos 2 θ gives us sin ⁡ 2 θ cos ⁡ 2 θ 1 = 1 cos ⁡ 2 θJustify your answers (b) For those equations that are identities, state and restrictions on the variables ( 1 − cos 2 x) ( 1 − tan 2 x) = sin 2 x − 2 sin 4 x 1 − sin 2 x (1 \cos^ {2}x) (1 \tan^ {2}x) = \frac {\sin^ {2}x 2\sin^ {4}x} {1 \sin^ {2}x} (1 −cos 2Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!

Precalculus Trigonometry Trig Identities 47 Of 57 Solve Tan 2 Theta 4 0 Theta Youtube

How Do You Verify 4tan 4 Tan 2x 3 Sec 2x 4tan 2x 3 Kinda Hard Please With All The Steps Thanks Socratic

Visit http//ilectureonlinecom for more math and science lectures!Following table gives the double angle identities which can be used while solving the equations You can also have #sin 2theta, cos 2theta# expressed in terms of #tan theta # as under #sin 2theta = (2tan theta) / (1 tan^2 theta)# #cos 2theta = (1 tan^2 theta) / (1 tan^2 theta)#There are various identities in trigonometry which are used for many trigonometric problems Let us see all the fundamental trigonometric identities here Reciprocal Identities Sin θ = 1/Csc θ or Csc θ = 1/Sin θ;

Trigonometric Identity Challenge Sin 2 Cos 2x Tan 2x Youtube

Sec 6x Tan 6x 1 2 Tan 2x Sec 2x Important Difficult Trigonometric Identity Youtube

The following integration problems use the method of trigonometric (trig) substitution It is a method for finding antiderivatives of functions which contain square roots of quadratic expressions or rational powers of the form n 2 (where n is an integer) of quadratic expressions Examples of such expressions are √4 − x2 and (x2 1)3 / 2Reciprocal Trigonometric Identities We already know that the reciprocals of sin, cosine, and tangent are cosecant, secant, and cotangent respectively Thus, the reciprocal identities are sin θ = 1/cosecθ (OR) cosec θ = 1/sinθTrigonometric cofunction identities are relationships between the basic trigonometric functions (sine and cosine) based on complementary anglesThey also show that the graphs of sine and cosine are identical, but shifted by a constant of π 2 \frac{\pi}{2} 2 π The identities are extremely useful when dealing with sums of trigonometric functions, as they often allow for use of the

Sec 2 Theta 1 Tan 2 Theta Youtube

3

Trigonometry Trigonometric identities PhysicsAndMathsTutorcom (b) (i) Using the identity cos (A B) ≡ cos A cos B – sin A sin B, prove that cos 2A ≡ 1 – 2 sin2 A (2) (ii) Hence solve, for 0 ≤ x < 2π, cos 2x = sin x, giving your answers in terms of π (5) (iii) Show that sin 2y tan y cos 2y ≡ 1, for 0 ≤ y < 2 1 π (3)Let's start with the left side since it has more going on Using basic trig identities, we know tan (θ) can be converted to sin (θ)/ cos (θ), which makes everything sines and cosines 1 − c o s ( 2 θ) = ( s i n ( θ) c o s ( θ) ) s i n ( 2 θ) Distribute the right side of the equation 1 − c o s ( 2 θ) = 2 s i n 2 ( θ)

Tangent Half Angle Formula Wikipedia

Use The Trigonometric Identities To Simplify The Chegg Com

Trigonometric Identities

Trigonometric Identities Simplify Expressions Video Lessons Examples And Solutions

Trigonometry Identities And Equations Ppt Download

Establish The Identity 1 Tan 2 Theta 1 Tan 2 Chegg Com

Trigonometric Identities Topics In Trigonometry

Lesson 22 Trigonometric Identities Ib Math Hl

Trigonometry Identities

Tangent Half Angle Formula Wikipedia

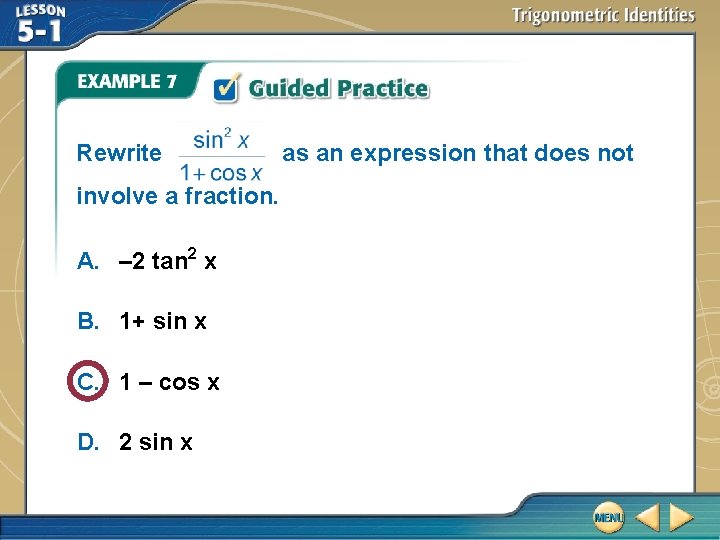
Lesson 5 1 Trigonometric Identities Fiveminute Check Over

Using Trigonometric Identities Video Khan Academy

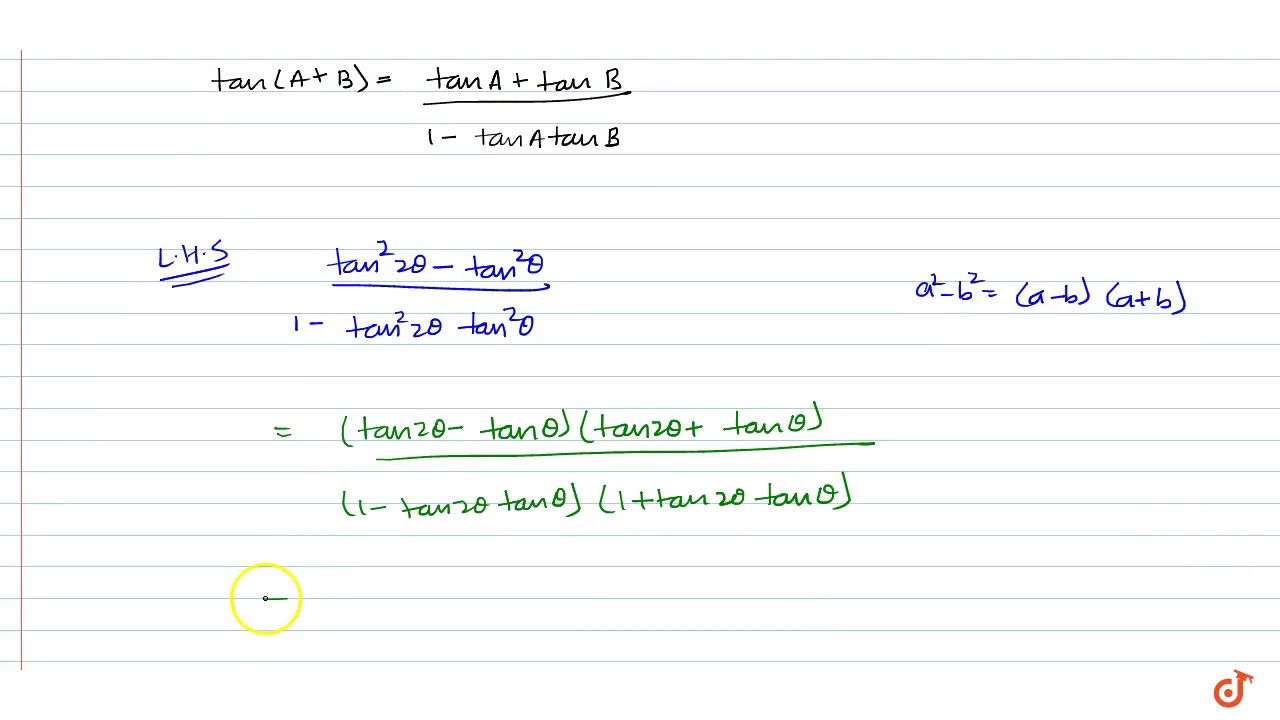
Prove That Tan 2 2theta Tan 2 Theta 1 Tan 2 2theta Tan 2 Theta Tan 3theta Tan Theta Youtube

Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download

Trigonometric Identities List Of Trigonometric Identities Examples

Rd Sharma Solutions For Class 10 Chapter 6 Trigonometric Identities Exercise 6 1 Get Pdf

Precalculus Trigonometry Trig Identities 29 Of 57 Formula For Lowering Power Tan 2 X Youtube

What Are The Quotient Identities For A Trigonometric Functions Socratic

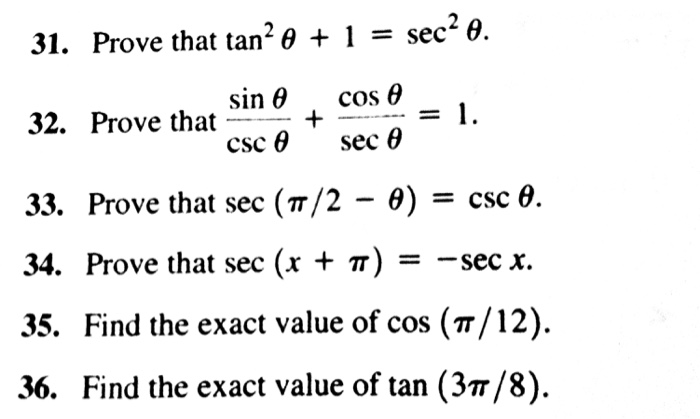
31 Prove That Tan 2 Theta 1 Sec 2 Theta 32 Chegg Com

Trigonometric Identities A Plus Topper

1

5 1 Fundamental Trig Identities Sin 1cos 1tan 1 Csc Sec Cot Csc 1sec 1cot 1 Sin Cos Ppt Download

How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic

Tan 2x Formula What Is Tan 2x Formula Examples

Ilectureonline

2 Prove The Following Trig Identities A Prove Tan Chegg Com

What Is Tan 2 Theta

Double Angle Formula And Half Angle Formula Video Lessons Examples And Solutions

How Do I Integrate Tan 2 X Youtube

Summary Of Trigonometric Identities

Trigonometric Identities Topics In Trigonometry

Integrate Sec 2x Method 2

Summary Of Trigonometric Identities

1 6 Trigonometric Review Ppt Video Online Download

Trigonometric Identities Trigonometric Functions Trigonometry

Trigonometric Identities

Trigonometric Identities Sin 2 X Cos 2 X Tan 2 X Youtube

Trigonometric Identities Examples

Sample Problems Cos 2 X Tan2 X Tan 2 Csc 2 Tan Sec X Tan X Cos X Sin 4 X Cos 4 X 1 2 Cos 2 X Pdf Free Download

Ch 7 Trigonometric Identities And Equations Ppt Video Online Download

Double Angle Formulas Trigonometry Teachoo 2x 3x Formula Provi

Section 2 1 Using Fundamental Identities Ppt Download

Use Trig Identities To Simplify Tan 2x Cot 2x A Gauthmath

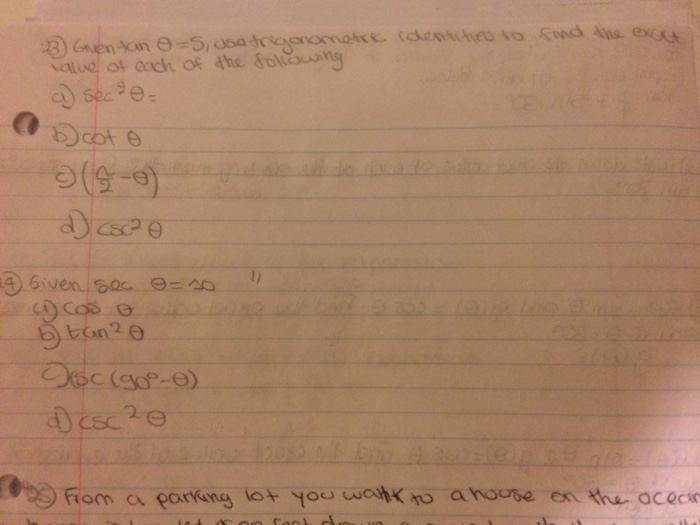
Given Tan Theta 5 Are Trigonometric Identities To Chegg Com

1 Tan 2x 1 Cos 2x Sin 2x 2sin 4x 1 Sin 2x Trigonometric Identities Mcr3u Youtube

What Is The Formula Of Tan2x Quora

Basic Trigonometric Identities

Proof Tan 2 1 Sec 2 Youtube

1 Point Use Trigonometric Identities To Simplify F Gauthmath

10 3 Verify Trigonometric Identities Ppt Video Online Download

5 1 5 2 Trigonometric Identities Ppt Download

6 2 Trigonometric Identities Trigonometry Siyavula

How To Solve Tan 2xsin 2x Tan 2x Sin 2x Trigonometry Trigonometric Identities Youtube

Tangent Half Angle Formula Wikipedia

Trigonometric Identities And Equations Ppt Download

10 Identity Tan Squared X 1 Sec Squared X Trigonometry Educator Com

How I Remember Trig Identities Part 2 Beyond Solutions

Complex And Trigonometric Identities Introduction To Digital Filters

Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube

Trig Identities Crossword Wordmint

How Do You Verify Tan 28 Sin 28 Tan 28sin 28 Socratic

Sample Problems Cos 2 X Tan2 X Tan 2 Csc 2 Tan Sec X Tan X Cos X Sin 4 X Cos 4 X 1 2 Cos 2 X Pdf Free Download

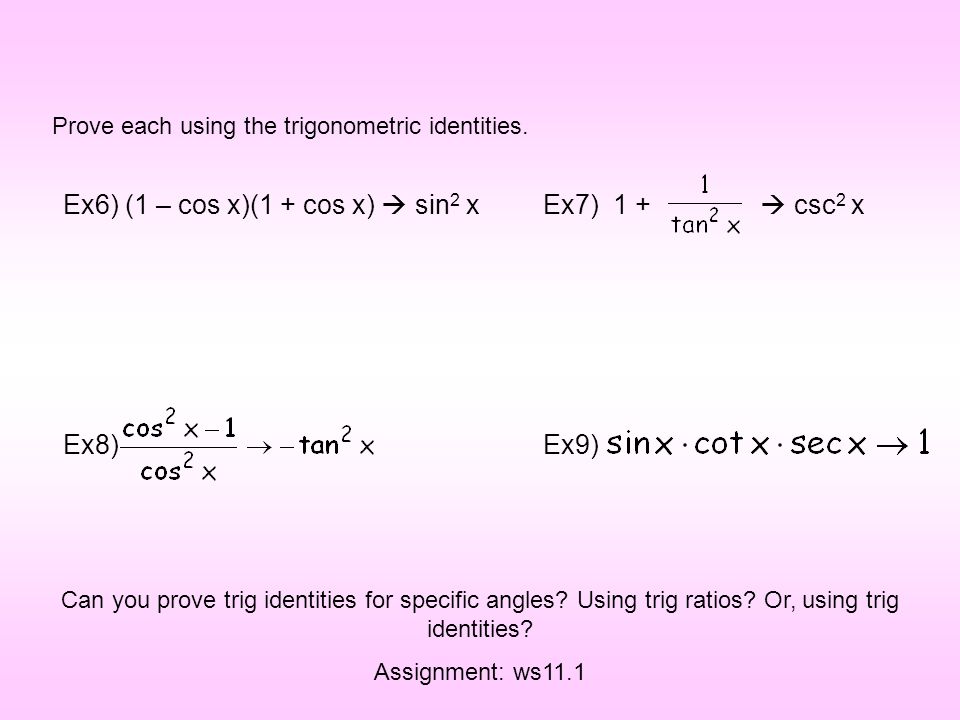
Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download

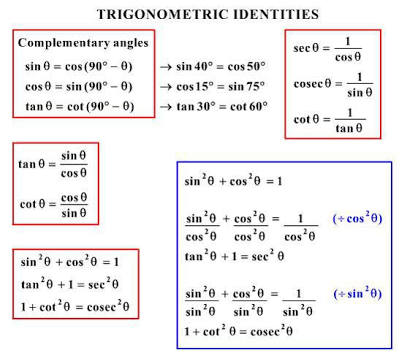
How Do You Simplify The Expression Sin 2theta Cos 2theta Cos 2theta Socratic

Trigonometric Identities A Plus Topper

Following Are A List Of Trigonometric Identities Chegg Com

Trigonometric Identity Review Trigonometry Identities Reciprocal Identities Sin 8 Cos 8 Tan 8 Quotient Identities Tan 8 Cot 8 Ppt Download

3

Trigonometric Identities A Plus Topper

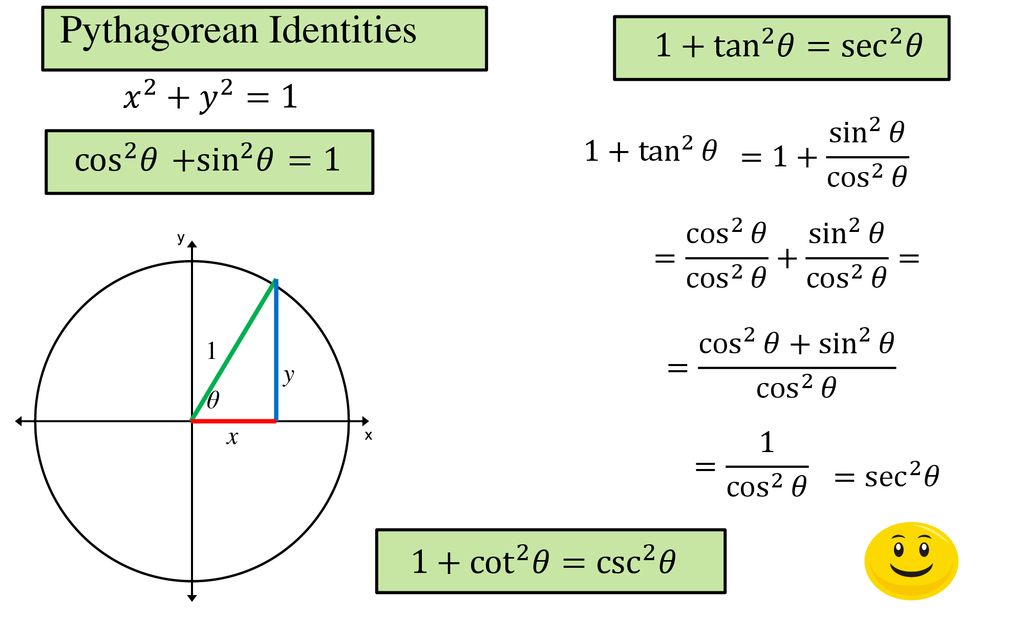
Trigonometric Identities And Equations Ppt Download

Integrate Tan 2x

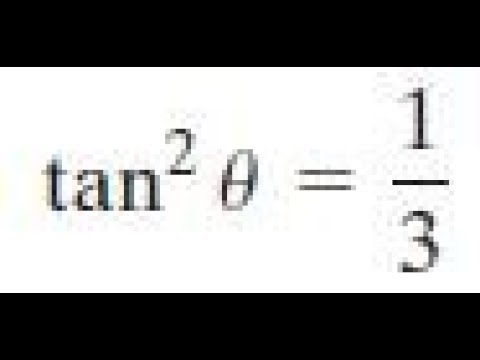
Tan 2 Theta 1 3 Solve For Interval 0 Less Theta Less 2pi Youtube

Trigonometric Identities A Plus Topper

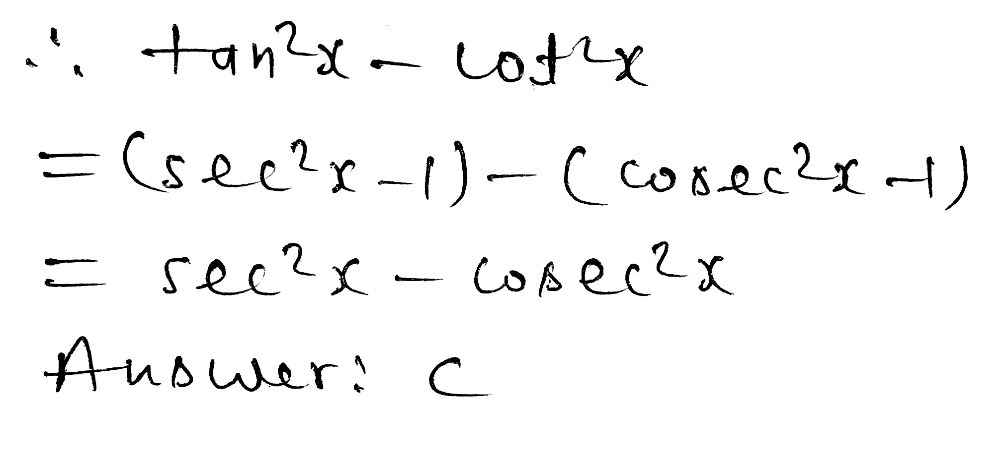
Use Trig Identities To Simplify Tan 2x Cot 2x A Gauthmath

How Do You Simplify Sec 4x Tan 4x Sec 2x Tan 2x Socratic

Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download

Incoming Term: trig identities tan^2 theta,